
But Big O notation focuses on the worst-case scenario, which is 0(n) for simple search. It’s a reassurance that simple search will never be slower than O(n) time. Algorithm running times grow at different rates. Assume that it takes 1 millisecond to check each element in the school district's database. Big-O Notation Cheat Sheet This cheat sheet shows the Big-O time and space complexities (runtime analysis) of common algorithms used in the computer science field. You can see which collection type or sorting algorithm to use at a glance to write the most efficient code. Asymptotic Notation is used to describe the running time of an algorithm - how much time an algorithm takes with a given input, n. There are three different notations: big O, big Theta (Θ), and big Omega (Ω). Big-Θ is used when the running time is the same for all cases, big-O for the worst case running time, and big-Ω for the best case running time.
| Sorting Algorithms | Space complexity | Time complexity | ||
|---|---|---|---|---|
| Worst case | Best case | Average case | Worst case | |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
| Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Shell Sort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Mergesort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quicksort | O(log n) | O(n log n) | O(n log n) | O(n log n) |
| Heapsort | O(1) | O(n log n) | O(n log n) | O(n log n) |
| Data Structures | Average Case | Worst Case | ||||
|---|---|---|---|---|---|---|
| Search | Insert | Delete | Search | Insert | Delete | |
| Array | O(n) | N/A | N/A | O(n) | N/A | N/A |
| Sorted Array | O(log n) | O(n) | O(n) | O(log n) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Doubly Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Stack | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Hash table | O(1) | O(1) | O(1) | O(n) | O(n) | O(n) |
| Binary Search Tree | O(log n) | O(log n) | O(log n) | O(n) | O(n) | O(n) |
| B-Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Red-Black tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| AVL Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| n f(n) | log n | n | n log n | n2 | 2n | n! |
|---|---|---|---|---|---|---|
| 10 | 0.003ns | 0.01ns | 0.033ns | 0.1ns | 1ns | 3.65ms |
| 20 | 0.004ns | 0.02ns | 0.086ns | 0.4ns | 1ms | 77years |
| 30 | 0.005ns | 0.03ns | 0.147ns | 0.9ns | 1sec | 8.4x1015yrs |
| 40 | 0.005ns | 0.04ns | 0.213ns | 1.6ns | 18.3min | -- |
| 50 | 0.006ns | 0.05ns | 0.282ns | 2.5ns | 13days | -- |
| 100 | 0.07 | 0.1ns | 0.644ns | 0.10ns | 4x1013yrs | -- |
| 1,000 | 0.010ns | 1.00ns | 9.966ns | 1ms | -- | -- |
| 10,000 | 0.013ns | 10ns | 130ns | 100ms | -- | -- |
| 100,000 | 0.017ns | 0.10ms | 1.67ms | 10sec | -- | -- |
| 1'000,000 | 0.020ns | 1ms | 19.93ms | 16.7min | -- | -- |
| 10'000,000 | 0.023ns | 0.01sec | 0.23ms | 1.16days | -- | -- |
| 100'000,000 | 0.027ns | 0.10sec | 2.66sec | 115.7days | -- | -- |
| 1,000'000,000 | 0.030ns | 1sec | 29.90sec | 31.7 years | -- | -- |
Sorting algorithms are a fundamental part of computer science. Being able to sort through a large data set quickly and efficiently is a problem you will be likely to encounter on nearly a daily basis.
Here are the main sorting algorithms:
| Algorithm | Data Structure | Time Complexity - Best | Time Complexity - Average | Time Complexity - Worst | Worst Case Auxiliary Space Complexity |
|---|---|---|---|---|---|
| Quicksort | Array | O(n log(n)) | O(n log(n)) | O(n^2) | O(n) |
| Merge Sort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort | Array | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort | Array | O(n) | O(n^2) | O(n^2) | O(1) |
| Select Sort | Array | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Bucket Sort | Array | O(n+k) | O(n+k) | O(n^2) | O(nk) |
| Radix Sort | Array | O(nk) | O(nk) | O(nk) | O(n+k) |
Another crucial skill to master in the field of computer science is how to search for an item in a collection of data quickly. Here are the most common searching algorithms, their corresponding data structures, and time complexities.
Big O Notation Chart
Here are the main searching algorithms:
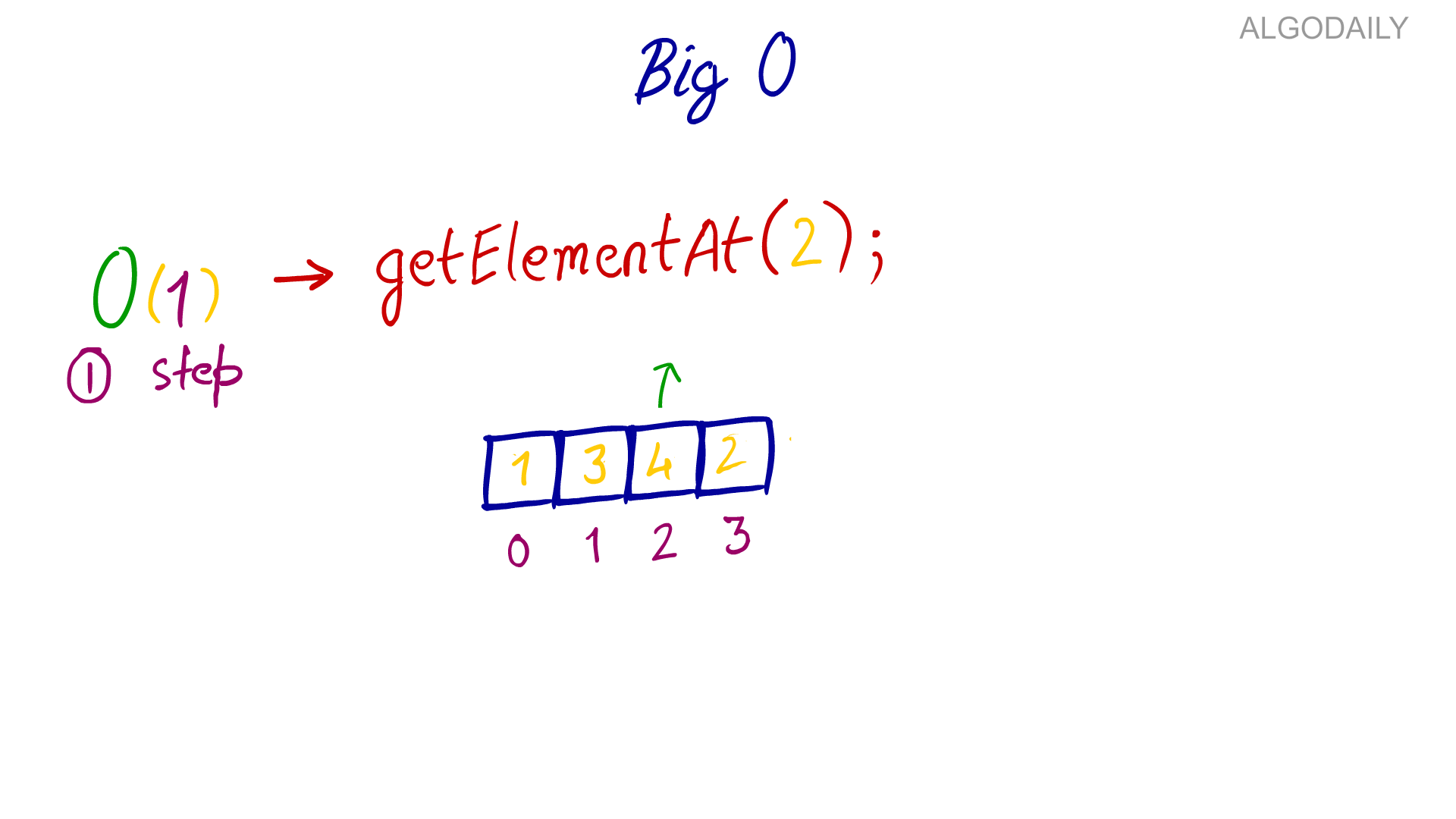
Big O Notation Cheat Sheet Python

| Algorithm | Data Structure | Time Complexity - Average | Time Complexity - Worst | Space Complexity - Worst |
|---|---|---|---|---|
| Depth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Breadth First Search | Graph of |V| vertices and |E| edges | - | O(|E|+|V|) | O(|V|) |
| Binary Search | Sorted array of n elements | O(log(n)) | O(log(n)) | O(1) |
| Brute Force | Array | O(n) | O(n) | O(1) |
| Bellman-Ford | Graph of |V| vertices and |E| edges | O(|V||E|) | O(|V||E|) | O(|V|) |
Graphs are an integral part of computer science. Mastering them is necessary to become an accomplished software developer. Here is the data structure analysis of graphs:
| Node/Edge Management | Storage | Add Vertex | Add Edge | Remove Vertex | Remove Edge | Query |
|---|---|---|---|---|---|---|
| Adjacency List | O(|V|+|E|) | O(1) | O(1) | O(|V| + |E|) | O(|E|) | O(|V|) |
| Incidence List | O(|V|+|E|) | O(1) | O(1) | O(|E|) | O(|E|) | O(|E|) |
| Adjacency Matrix | O(|V|^2) | O(|V|^2) | O(1) | O(|V|^2) | O(1) | O(1) |
| Incidence Matrix | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|E|) |
Storing information in a way that is quick to retrieve, add, and search on, is a very important technique to master. Here is what you need to know about heap data structures:

Big 0 Notation Cheat Sheet Template
| Heaps | Heapify | Find Max | Extract Max | Increase Key | Insert | Delete | Merge |
|---|---|---|---|---|---|---|---|
| Sorted Linked List | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Unsorted Linked List | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap | - | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) |
| Fibonacci Heap | - | O(1) | O(log(n))* | O(1)* | O(1) | O(log(n))* | O(1) |
