
Trishear in 3D
Trishear is a kinematic model of fault propagation folding in which the decrease in displacement along the fault is accommodated by heterogeneous shear in a triangular zone radiating from the tip line. A thorough review of the model and its applications is given by Hardy and Allmendinger (2011).
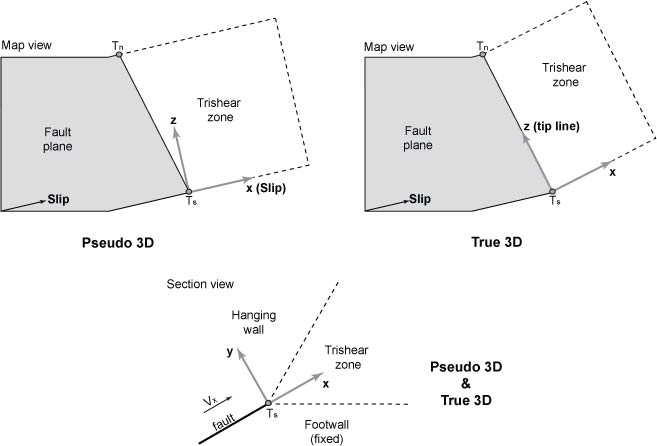
Trishear has been extended to three dimensions using two kind of formulations: A pseudo-3D formulation in which the model is solved in serial cross sections all parallel to the slip direction (Cristallini and Allmendinger, 2001), and a true-3D formulation in which the kinematics is solved in three dimensions assuming volume conservation (Cristallini et al., 2004). The true-3D algorithm is based on an xyz coordinate system with x perpendicular to the tip line, y perpendicular to the fault plane (i.e. pole to the fault), and z parallel to the tip line. The figure below shows the coordinate system and solution strategy of the pseudo and true-3D algorithms. More details about the algorithms and their implementation can be found in Cardozo, 2008.
Trishear3D is a Macintosh program to run 3D trishear models. The program also computes the finite strain based on tetrahedrons embedded in the model. Model parameters can be set up at the start of the simulation and modified at any stage (i.e. Fault geometry and trishear parameters can be modified and beds can be added). Academia.edu is a platform for academics to share research papers.
Coordinate systems of the pseudo and true-3D trishear models
I have implemented these algorithms in a computer program called Trishear3D. Trishear3D is a Macintosh program to run 3D trishear models. The program also computes the finite strain based on tetrahedrons embedded in the model. Model parameters can be set up at the start of the simulation and modified at any stage (i.e. fault geometry and trishear parameters can be modified and beds can be added). Geometry and strain can be visualized in a 3D plot that can be easily manipulated, sliced, and queried for geometry or strain data. Geometry and strain can also be examined as tables. These tables can be exported to fracture or reservoir modeling software. Trishear3D is a great tool to investigate the effects of spatial and temporal variations of fault parameters on the geometry and strain field of the associated fold(s).
I will discuss here a couple of models that illustrate the complexity of the geometry and finite strain of 3D trishear like folds. The first set of simulations illustrate the effects of varying fault slip, trishear angle, or propagation to slip (P/S) ratio along the fault. In the figure below the upper left model is a trishear model of a 60º dipping, normal fault, with no variation of trishear parameters. The upper right model is similar but includes a linear variation of slip along the fault. The lower left model includes a linear variation of trishear angle along the fault, and the lower right model includes a linear variation of P/S along the fault. All models were made with the pseudo-3D algorithm. In the three models with variation of trishear parameters, the parameter is maximum at the right. The beds are colored by the magnitude of finite strain (maximum stretch).
Pseudo-3D trishear models without (upper left) and with variation of trishear parameters
The variation of trishear parameters results in complex geometry and strain fields. In general, the strain is higher in regions with higher slip, lower trishear angle, and lower P/S ratio. Geometry and strain varies along the fault, but also with stratigraphic level. In the variable P/S simulation (lower right model), the strain is higher to the right of the model (high P/S) in the upper layers, and to the left of the model (low P/S) in the lower layers.
Trishear in 3D adds another interesting possibility: lateral fault propagation. The fault can grow not only along dip, but also along strike. In Trishear3D lateral fault propagation is implemented by setting the dip slip in one of the fault tips to zero, and moving this fault tip along strike according to a prescribed lateral P/S ratio. The figure below shows a simulation of a normal relay ramp. The bed is colored by finite strain (maximum stretch).

The geometry and strain of the resulting ramp is quite complex. There is interaction between the faults. The magnitude of the strain and the orientation of the intermediate strain axis across the ramp (not shown in the figure), coincides with the observed density and orientation of deformation bands across a relay ramp in Arches National Park, Utah (Rotevatn, 2006).
Current research
Sigurd Aanonsen and I, have written several Matlab scripts to do trishear inverse modeling, i.e. Estimating the trishear parameters that best fit a structure. These scripts rely on several optimization algorithms that speed-up the parameters estimation significantly. We can now conduct 2D and 3D trishear parameters estimations (six or more parameters) in seconds. Optimized trishear inverse modeling has allowed us to address questions such as the uncertainties of the estimated parameters (Cardozo and Aanonsen, 2009).
A natural extension of this work is the application of the optimized trishear inversion algorithms to trishear-like 2D fold profiles and 3D fold surfaces from outcrops or seismic. In collaboration with Paul Whipp and Chris Jackson at Imperial College, we have applied the algorithms to surface structural data along the Hadadid monocline, Gulf of Suez, Egypt.
Improving the robustness of the algorithms is also important. I implemented a more robust optimized trishear inversion using simulated annealing. We have used this technique to evaluate the uniqueness of trishear models. Rather than searching for a best-fit model, the aim of the algorithm is to search for the range of possible models that might fit a structure. This methodology is a better approach for modeling structural data and their uncertainties (see Cardozo et al., 2011).
In collaboration with Karl Mueller and Pamela Grothe at the University of Colorado, we have used this latest algorithm to infer the history of slip and propagation of the Osaka Bay fault in Japan (Grothe et al., 2014). Also with J.P. Brandenburg at Shell, we have used a similar strategy to model listric propagating thrusts (Cardozo and Brandenburg, 2014).
References
Cardozo, N., Jackson, C. and Whipp, P. 2011. Determining the uniqueness of best-fit trishear models. Journal of Structural Geology 33, 1063-1078.
Cardozo, N. and Aanonsen, S.I. 2009. Optimized trishear inverse modeling. Journal of Structural Geology 31, 546-560.
Cardozo, N. 2008. Trishear in 3D: Algorithms, implementation, and limitations. Journal of Structural Geology 30, 327-340.
Cardozo, N. and Brandenburg, J.P. 2014. Kinematic modeling of folding above listric propagating thrusts. Journal of Structural Geology 60, 1-12.
Cristallini, E.O. and Allmendinger, R.W. 2001. Pseudo-3D modeling of trishear fault-propagation folding. Journal of Structural Geology 23, 1883-1899.
Cristallini, E.O., Giambiagi, L. and Allmendinger, R.W. 2004. True three-dimensional trishear: A kinematic model for strike-slip and oblique deformation. Geological Society of America Bulletin 116, 938-952.
Grothe, P.R., Cardozo, N., Mueller, K. and Ishiyama, T. 2014. Propagation history of the Osaka-wan blind thrust, Japan, from trishear modeling. Journal of Structural Geology 58, 79-94.
Hardy, S. and Allmendinger, R.W. Trishear: A review of kinematics, mechanics and applications. 2011. In McClay, K., Shaw, J.H. and Suppe, J. (Eds).Thrust Fault Related Folding: American Association of Petroleum Geologists, Memoir 94, 95-121.
Trishear
- Directory
- Reservoir Engineering
- Reservoir Simulation
- Articles
- Technical Articles
- Marketing Articles
Profile Details


Similar Oil And Gas Software
- Profile Name: Petrel Geoscience CoreCountry: USAHits: 1,392Visited: 312
- Profile Name: Petrel Well CorrelationCountry: USAHits: 2,949Visited: 430
- Profile Name: Techlog Wellbore ImagingCountry: USAHits: 1,473Visited: 306
- Profile Name: Petrel Structural Framework BuilderCountry: USAHits: 1,966Visited: 361
Trisheary
PetroMehras Services
